Magnetic Shielding
The purpose of magnetic shielding is to protect an instrument from this magnetic field, in order to ensure optimal operation, or to protect an environment from a magnetic field emitted by an instrument and/or an energy source. Similarly, an instrument may itself emit a magnetic field that can create significant interference with electrical devices. If the assets are not shielded, then the magnetic flux can interfere with the operation.
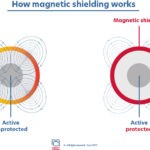
There are two types of magnetic shielding that are complementary:
- Active shielding
Passive shielding
In the case of passive shielding (MECA MAGNETIC’s core business), the magnetic field can be absorbed by a metal shield.
In the case of active shielding, the magnetic field can also be neutralized by another instrument which emits an opposite magnetic field of equivalent value, thus eliminating the residual field in a limited space. The know-how of a shielding consists in selecting one of these two solutions, and sometimes combining them, when the residual field requirement of a space is very low, which is a competence of MECA MAGNETIC.
A passive magnetic shield can be considered as a Faraday cage for continuous or low frequency magnetic fields. Unlike a Faraday cage, we try to prevent a field from entering or leaving a volume or to channel it into a dedicated volume. Only certain materials have a high magnetic permeability or magnetic susceptibility and a low coercive field to limit the effects of hysteresis, namely permimphy or other iron nickel alloys. A material with a high magnetic susceptibility will tend to concentrate the magnetic field lines.
The principle of passive shielding
Magnetic shielding is a mechanical solution, most of the time coming from a sheet metal part, intended to solve a problem of low frequency electromagnetic disturbance. It is then called “passive shielding”.
A shielding conducts the magnetic component of the electromagnetic wave on frequencies from 0.1 to 10,000 Hz. Above 10,000 Hz, electrical shields made of other materials and requiring other designs are used.
- The purpose of a shield is to attract, concentrate and deflect magnetic field lines. It can thus prevent them from coming into a given volume (e.g. the shielding of a cathode ray tube) or prevent a magnetic field from propagating (e.g. the shielding of a transformer).
A field line is not stored, does not stop and always loops back. It will propagate in the environment where the permeability is the most important.
Unlike electrical shielding, magnetic shielding consists of deflecting the field lines, so a simple plate constitutes a shield.
Designing a magnetic shield
The usual checks
Before starting to look for a solution, the following points should be checked:
- – Am I in a DC field or an AC field?
- – Am I in a weak or strong field?
- – Is it necessary to shield the pollution or the sensitive part?
- – What attenuation should I have?
- – Are the values given or measured reliable?
- – Are these values given as average values or peak values?
- – How much space is available for shielding?
- – What other parameters must I take into account: ventilation, cable routing, mechanical or climatic stress, accessibility, etc.?
Design methods
Different design methods are possible:
- – From fairly simple formulas, which can very quickly give, in continuous field, an idea of the solution.
- – From more complex formulas (using abacuses), formalized among others by Albrecht J. MAGER in 1970 who, from simple forms, refines solutions in DC or AC.
- – From finite element simulations (integrating Maxwell’s equations); this solution remains an approach intended for complex shapes and depends greatly on the mesh and the B-H curves of the materials integrated into the software
The design and the attenuation requirement will allow to identify a possible complementary need for active shielding.

Which material for which shielding result?

Thicknesses worked
Single layer versus multilayer
The attenuation of the magnetic field required is one of the criteria for choosing the thickness of the material selected and the choice between monolayer and multilayer. The second criterion is the constraint linked to the surface to be shielded and/or the residual surface required.
- A multilayer is a specific know-how mastered at MECA MAGNETIC. It consists of a succession of shields assembled on the principle of Russian dolls. It is assumed that two 1 mm layers separated by an air gap are more effective than one 2 mm layer (analogy with double glazing).
It is used when the fields are high or when we are looking for an important attenuation. Layer after layer, the field strength decreases significantly. This avoids saturation phenomena and allows extremely low residual field strength values to be achieved. This is the ideal solution for zero field chambers. Compared to the earth’s field, attenuations of a factor of 10,000 can be achieved, resulting in residual fields of a few nano tesla.

Current regulations
A European directive on electromagnetic fields was issued in June 2013: 2013/35/EU
Each European country can have, at the national level, a regulation stricter than this European regulation. This is the case in France, for example, with Decree No. 2013-1162 – Decree No. 2013-1162 of December 14, 2013, which defines a stricter framework for certain sensitive environments (hospitals, schools …).
Q&A
The magnetic field is a physical phenomenon generated by the displacement of electric charges and revealed by magnetic materials.
To isolate the mechanism from the magnetic field of the magnet, it is necessary either to enclose the magnet in a cage of FARADAY, or to enclose the mechanism in it.
The magnetic field passes through everything, walls, concrete, granite, the human body… and cannot be stopped. The only solution to protect yourself from it is to move away from the source.
Yes, magnetic shielding is possible by using materials with high magnetic susceptibility, which concentrate the magnetic field lines so that they remain within the material.
It is a protection against magnetic waves which allows to attenuate in a defined volume the ambient magnetic field.
By using a material capable of concentrating the magnetic field lines created in space by magnetic field sources, such as magnets.
Both. Either you don’t want a sensitive element to be disturbed, or you don’t want an element to disturb.
Any frequency can be shielded using different techniques. For low frequencies, we use materials with high permeability; for higher frequencies we use materials with low resistivity.
For very high frequencies (Giga hertz), the use of plastic-filled paint or other is more suitable.
Delay in the development of a physical phenomenon compared to another